No deserto da Nlogônia, uma longa caravana de camelos carregados de especiarias está parada num oásis para descansar. O chefe da caravana notou que alguns camelos pareciam mais cansados do que os outros, e descobriu que cada camelo estava carregando um peso diferente, de forma que alguns camelos carregam um peso muito maior do que outros e portanto se cansam mais. Aproveitando a parada para descanso, o chefe da caravana quer redistribuir as especiarias entre os camelos, de forma que todos os camelos carreguem exatamente o mesmo peso. Dados os pesos carregados por cada camelo antes da parada, escreva um programa que determine, para cada camelo, qual o peso que deve ser retirado ou adicionado, para que todos carreguem exatamente o mesmo peso.

Entrada

A primeira linha contém um inteiro N, o número de camelos na caravana. Os camelos são numerados de 1 a N. Cada uma das linhas seguintes contém um inteiro Pi , o peso que o camelo de número i carregava antes da parada. Os camelos são dados em ordem crescente de numeração.

Saída

Para cada camelo da caravana, seu programa deve produzir uma linha, o valor que deve ser adicionado ou retirado desse camelo para que todos os camelos carreguem o mesmo peso. A ordem dos camelos na saída deve ser a mesma ordem dada na entrada. Para todos os casos de teste o peso que cada camelo deve carregar é um número inteiro.

Restrições • 1 ≤ N ≤ 1 000 • 1 ≤ Pi ≤ 10 000 para 1 ≤ i ≤ N

Exemplo de entrada

1 3 100 104 108

Exemplo de saída

1 4 0 -4

Ref: 0001/04/23

Joãozinho te propôs o seguinte desafio: ele escolheu dois inteiros A e B, com 1 ≤ A ≤ B ≤ 101000, e escreveu na lousa todos os inteiros entre A e B, em sequência, porém colocando um espaço após cada dígito, de forma a não ser possível ver quando um número termina ou começa. Por exemplo, se Joãozinho escolher A = 98 e B = 102, ele escreveria a sequência “9 8 9 9 1 0 0 1 0 1 1 0 2”. Seu desafio é: dada a lista de dígitos escritos na lousa, encontrar os valores de A e B. Caso exista mais de uma possibilidade para os valores que geraria a lista, você deve encontrar uma em que o valor de A é o menor possível. É garantido que a lista de dígitos da lousa tem no máximo tamanho 1000.

Entrada

A primeira linha da entrada contém um único inteiro N, indicando o número de dígitos. A segunda linha contém N inteiros di, indicando os dígitos escritos.

Saída

Imprima o menor valor possível de A. Restrições • 1 ≤ N ≤ 1000 • 0 ≤ di ≤ 9 Informações sobre a pontuação • Para um conjunto de casos de testes valendo 21 pontos, 1000 ≤ A ≤ B ≤ 9999. • Para outro conjunto de casos de testes valendo 23 pontos, B = A + 1. • Para outro conjunto de casos de testes valendo 40 pontos, A, B < 106 . • Para outro conjunto de casos de testes valendo 16 pontos, nenhuma restrição adicional.

Exemplo de entrada

6 1 2 3 1 2 4

Exemplo de saída

123

Ref: 0002/04/23

Um quadrado fantástico é um conjunto de números inteiros positivos dispostos em N linhas por N colunas, tal que: • Não há números repetidos no quadrado. • A média dos números em cada linha é um número inteiro que está presente na linha. • A média dos números em cada coluna é um número inteiro que está presente na coluna.

Entrada

A primeira e única linha da entrada contém um número inteiro N, indicando a dimensão do quadrado.

Saída

Seu programa deve produzir N linhas, cada uma contendo N números inteiros Xi , representando um quadrado fantástico.

Restrições • 1 ≤ N ≤ 40 • 1 ≤ Xi ≤ 1000000

Informações sobre a pontuação • Para um conjunto de casos de testes valendo 44 pontos, 1 ≤ N é ímpar. • Para outro conjunto de casos de testes valendo 56 pontos, nenhuma restrição adicional.

Exemplo de entrada

1

Exemplo de saída

1

Ref: 0003/04/23

Um quadrado fantástico é um conjunto de números inteiros positivos dispostos em N linhas por N colunas, tal que: • Não há números repetidos no quadrado. • A média dos números em cada linha é um número inteiro que está presente na linha. • A média dos números em cada coluna é um número inteiro que está presente na coluna.

Entrada

A primeira e única linha da entrada contém um número inteiro N, indicando a dimensão do quadrado.

Saída

Seu programa deve produzir N linhas, cada uma contendo N números inteiros Xi , representando um quadrado fantástico.

Restrições • 1 ≤ N ≤ 40 • 1 ≤ Xi ≤ 1000000

Informações sobre a pontuação • Para um conjunto de casos de testes valendo 44 pontos, 1 ≤ N é ímpar. • Para outro conjunto de casos de testes valendo 56 pontos, nenhuma restrição adicional.

Exemplo de entrada

1

Exemplo de saída

1

Ref: 0004/04/23

Seja N o menor número inteiro positivo que multiplicado por 33 resulta em um número cujos algarismos são todos iguais a 7. Determine a soma dos algarismos de N.

Ref: 0005/04/23

Sejam r e s números inteiros. Sabe-se que a equação do segundo grau

x² – (r + s)x + rs + 2010 = 0

tem as duas soluções inteiras. Quantos são os possíveis valores de |r – s|?

Ref: 0006/04/23

Diamantino gosta de jogar futebol, mas se jogar dois dias seguidos ele fica com dores musculares. De quantas maneiras Diamantino pode escolher em quais de dez dias seguidos ele vai jogar bola sem ter dores musculares? Uma maneira é não jogar futebol em nenhum dos dias.

Ref: 0007/04/23

Resolva o sistema

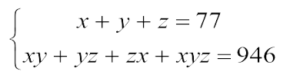
sendo x ≤ y ≤ z inteiros não negativos.

Ref: 0008/04/23

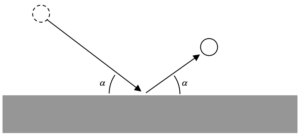
Uma mesa de bilhar tem o formato de um quadrado ABCD. SuperPablo tem uma missão especial: ele deve dar uma tacada em uma bola de bilhar, inicialmente colocada no vértice A, de modo que, após bater exatamente 2010 vezes nos lados do quadrado, a bola chegue, pela primeira vez, a um vértice do quadrado.

Quantos são os possíveis valores do ângulo formado pelo lado AB com a trajetória inicial da bola?

Observação: ao bater nos lados do quadrado, a bola sofre reflexão perfeita, ou seja, o ângulo de incidência é igual ao ângulo de reflexão. Suponha também que a bola seja um ponto.

Ref: 0009/04/23